علوم و مهارت های ریاضی به طور گسترده ای به عنوان کلیدهای پیشرفت اقتصادی و فناوری مورد تحسین قرار می گیرند، اما ریاضیات محض ممکن است از کاربرد های عملی خود در زمینه های مختلف مانند موارد صنعتی و پزشکی ، دور باشد.
به گزارش تکناک، ریاضیات محض اغلب کاربردهای پیش بینی نشده ای به همراه دارد، اما بدون ماشین زمان برای نگاه کردن به آینده، ریاضیدانانی چگونه انتخاب می کنند که چه چیزی را مطالعه کنیم؟
غالبا” از برخی ریاضیدانان پرسیده می شود که چه چیزی یک مسئله ریاضی را جالب می کند، و آنها پیشنهادات زیادی ارائه کردند: شگفتی ها، تضادها، الگوها، استثناها، موارد خاص، ارتباطات. این پاسخ ها ممکن است کاملاً متفاوت به نظر برسند، اما همه آنها از دیدگاه جهان ریاضی به عنوان ساختاری برای کاوش پشتیبانی می کنند.
در این دیدگاه، ریاضیدانان مانند آناتومیستهایی هستند که یاد میگیرند یک بدن چگونه کار میکند، یا دریانوردانی که مسیرهای آبهای جدید را ترسیم میکنند. سؤالاتی که ما میپرسیم اشکال مختلفی دارند، اما جالبترین سؤالها آنهایی هستند که به ما کمک میکنند یک تصویر بزرگ را واضحتر ببینیم.
ساختن نقشه ها
موضوعات ریاضی اشکال مختلفی دارند. برخی از آنها احتمالاً کاملاً آشنا هستند، مانند اعداد و اشکال. برخی دیگر ممکن است عجیب تر به نظر برسند، مانند معادلات، توابع و تقارن.
به جای نامگذاری فقط اشیاء، یک ریاضیدان ممکن است بپرسد که دسته ای از اشیاء چگونه سازماندهی شده اند. اعداد اول را در نظر بگیرید: ما می دانیم که تعداد بی نهایت زیادی از آنها وجود دارد، اما ما به درک ساختاری نیاز داریم تا بفهمیم این اعداد به دفعات رخ می دهند یا آنها را به روشی کارآمد شناسایی کنیم.
سؤالات خوب دیگر روابط بین اشیاء ظاهراً متفاوت را بررسی می کنند. به عنوان مثال، اشکال تقارن دارند، و راه حل های برخی معادلات نیز متقارن هستند.
طبقه بندی اشیاء و یافتن ارتباط بین آنها به ما کمک می کند تا نقشه ای منسجم از دنیای ریاضی جمع آوری کنیم. در طول مسیر، گاهی اوقات با نمونههای شگفتانگیزی مواجه میشویم که الگوهای کشف شده ما را به چالش میکشند.
چنین تناقضات ظاهری نشان می دهد که درک ما هنوز در کجا مشکل دارد و حل آنها بینش ارزشمندی را ارائه می دهد.
مثلث را در نظر بگیرید
مثلث مثال معروفی از یک تضاد ظاهری را ارائه می دهد. اکثر مردم مثلث را شکلی می دانند که توسط اتصال سه خط تشکیل شده است، و این برای هندسه ای که می توانیم روی یک صفحه کاغذ ترسیم کنیم، به خوبی کار می کند.
با این حال، این مفهوم از مثلث محدود است. در سطحی بدون خطوط مستقیم، مانند یک کره یا برگ کلم پیچ، به تعریف انعطافپذیرتری نیاز داریم.
بنابراین، برای گسترش هندسه به سطوحی که مسطح نیستند، یک ریاضیدان با ذهن باز ممکن است تعریف جدیدی از مثلث ارائه دهد. سه نقطه را انتخاب کنید و هر جفت را با کوتاه ترین مسیر بین آنها وصل کنید.
این یک تعمیم عالی است زیرا با تعریف آشنا در محیط آشنا مطابقت دارد، اما گستره جدیدی را نیز باز می کند. هنگامی که ریاضیدانان برای اولین بار این مثلث های تعمیم یافته را در قرن نوزدهم مطالعه کردند، معمایی هزاران ساله را حل کردند و انقلابی در ریاضیات ایجاد کردند.
اصل توازی اقلیدس
در حدود 300 سال قبل از میلاد، ریاضیدان یونانی اقلیدس رساله ای در مورد هندسه مسطح به نام عناصر نوشت. این کار هم اصول اساسی و هم نتایجی را ارائه میکند که به طور منطقی از آنها استخراج شده است.
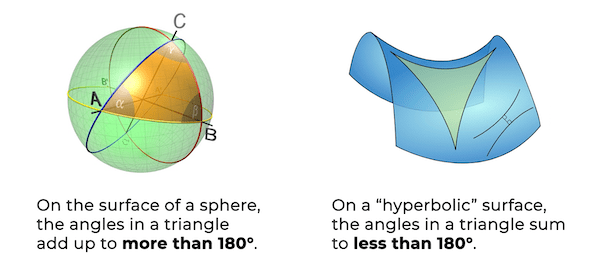
یکی از اصول او که اصل موازی نام دارد، معادل این جمله است که مجموع زوایای هر مثلث 180 درجه است. این دقیقاً همان چیزی است که شما در هر مثلث مسطح اندازه گیری می کنید، اما ریاضیدانان بعدی بحث کردند که آیا اصل توازی باید یک اصل اساسی باشد یا فقط یک نتیجه از سایر مفروضات اساسی.
این معما تا سال 1800 ادامه داشت، زمانی که ریاضیدانان متوجه شدند که چرا یک اثبات تا این حد مبهم مانده است: اصل توازی اقلیدس در برخی از سطوح نادرست است.
در یک کره، اضلاع یک مثلث از یکدیگر خم میشوند و مجموع زوایای آن بیش از 180 درجه می شود. روی یک برگ کلم پیچ موجدار، دو طرف به سمت یکدیگر خم می شوند و مجموع زاویه آن کمتر از 180 درجه می شود.
وجود مثلث هایی که مجموع زاوایای آنها از قاعده ظاهری تبعیت نمی کند ، منجر به آشکار سازی این موضوع شد که انواعی از هندسه وجود دارد که اقلیدس هرگز تصور نمی کرد. این یک حقیقت عمیق است، با برنامه های کاربردی در فیزیک، گرافیک کامپیوتری، الگوریتم های سریع و فراتر از آن.
روزهای آغازین
مردم گاهی اوقات در مورد این موضوع بحث می کنند که آیا ریاضیات کشف یا ابداع شده است؟ اما هر دو دیدگاه حقیقت دارد. در واقع انتخاب سؤالاتی که باید مطالعه کنیم، کار خلاقانه ای است.
سوالات جالبی از اختلاف بین الگوهایی که ما درک می کنیم و استثناهایی که آنها را به چالش می کشند، ناشی می شوند. پیشرفت زمانی حاصل می شود که تضادهای ظاهری تطبیق داده شوند تا راه برای شناسایی تضاد های جدید هموار شود.
امروزه ما(ریاضی دانان) هندسه سطوح دو بعدی را به خوبی درک می کنیم، بنابراین آماده شده ایم تا خود را در برابر سؤالات مشابه در مورد اجسام با ابعاد بالاتر آزمایش کنیم.
در چند دهه گذشته ما آموخته ایم که فضاهای سه بعدی نیز هندسه ذاتی خود را دارند. جالب ترین آنها هندسه هذلولی نام دارد و به نظر می رسد مانند یک نسخه سه بعدی از کلم پیچ عمل می کند. ما می دانیم که این هندسه وجود دارد، اما همچنان مرموز است. در زمینه تحقیقاتی ، سؤالات زیادی وجود دارد که می توانیم برای هر فضای سه بعدی به جز موارد هذلولی پاسخ دهیم.
در ابعاد بالاتر هنوز سوالات زیادی داریم که پاسخ آنها هنوز یافت نشده است، اما به جرات می توان گفت که مطالعه هندسه چهار بعدی وارد روزهای جوانی خود می شود.