ریاضیدانان دانشگاه موناش پس از ۳۸۰ سال، دایرههای دکارت یکی از مسائل کلاسیک دنیای هندسه را سرانجام با کمک روشهایی برگرفته از فیزیک نظری حل کردند.
به گزارش تکناک، این ریاضیدانان تعمیمی بیسابقه از مسئله دایرههای دکارت ارائه دادند و معادلهای کلی برای پیکربندیهای پیچیدهتر از چهار دایره مماس معرفی کردند.
مسئله دایرههای دکارت (Descartes’ Circle Theorem) به ارتباط بین شعاع یا انحنای چهار دایره مماس با یکدیگر میپردازد. این مسئله مربوط به حالتی است که سه دایره به صورت مماس با یکدیگر قرار دارند و میخواهیم دایره چهارمی بیابیم که با هر سه دایره دیگر نیز مماس باشد.
این پژوهش به رهبری دکتر دانیل ماتیوز، دانشیار دانشکده ریاضیات دانشگاه موناش و با همکاری اوریون زیماریس، دانشجوی دکترا انجام شده است. آنها موفق شدند که با استفاده از اسپینورها، که مفهومی کلیدی در مکانیک کوانتومی و نظریه نسبیت هستند، الگوی هندسی موسوم به «n-گل» را به صورت دقیق توصیف کنند.
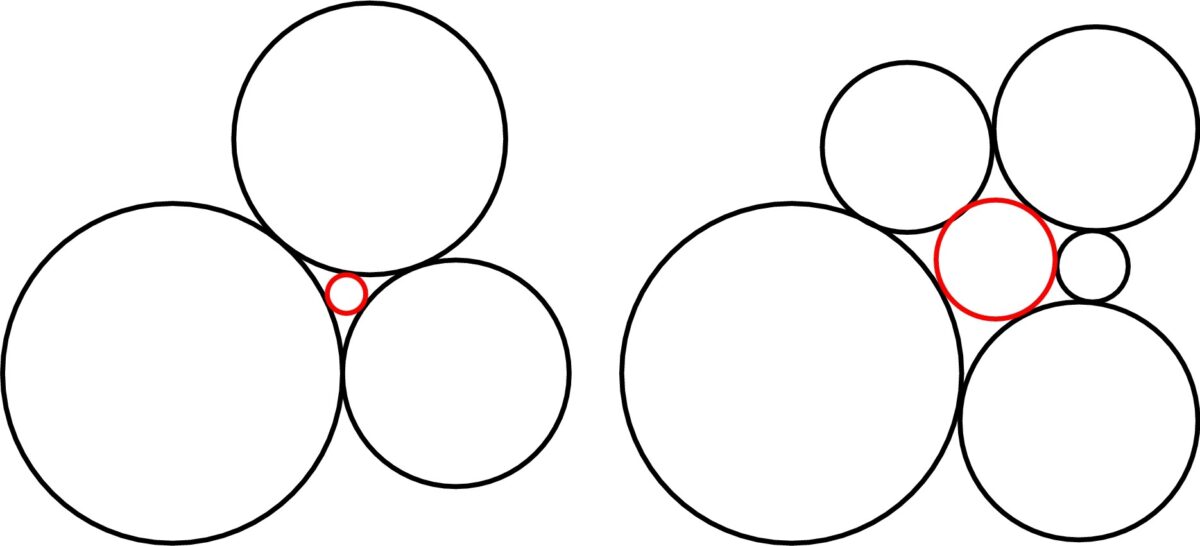
در نظریه چیدمان دایرهای، الگوی «گل» به پیکربندی خاصی از دایرههای مماس گفته میشود که در آن دایرهای مرکزی با چندین دایره بیرونی (گلبرگ) احاطه شده است. مشخص بودن خمیدگی گلبرگها، امکان تعیین دقیق خمیدگی دایره مرکزی را فراهم میکند. اما تا پیش از این، معادلهای کلی برای تعیین رابطه میان خمیدگیها در پیکربندیهای بیش از چهار دایره ارائه نشده بود.
مسئله دکارت که برای نخستینبار در قرن هفدهم مطرح شد، به رابطه میان چهار دایره مماس اشاره دارد و از آن زمان تاکنون پایهای برای مطالعه بسیاری از مسائل هندسی بوده است. این معادله در طول تاریخ توسط ریاضیدانانی مانند: یاماجی نوشیزومی (۱۷۵۱)، یاکوب اشتاینر (۱۸۲۶)، ویلیام بیکرافت (۱۸۴۲) و فردریک سادی (۱۹۳۶) بازتفسیر و بازکشف شده است.
ماتیوز در توضیح این پژوهش گفت:
«دکارت در سال ۱۶۴۳ مسئلهای را برای شاهدخت الیزابت از پالاتین مطرح کرد، با این تصور که خود او قادر به حل آن است، اما موفق نشد. نسخه سادهسازیشدهای از آن مسئله بعدها به عنوان مسئله کلاسیک دایرههای دکارت شناخته شد.»
زیماریس که تحقیق دکترای او به این دستاورد انجامیده است، بیان کرد: «روشی که به کار گرفتیم، بر پایه ابزارهای هندسی پیشرفتهای بود که الهامگرفته از فیزیک هستند. شگفتآور است، اسپینورهایی که برای توصیف چرخش کوانتومی و نسبیت به کار میروند، بتوانند چیدمان دایرهها را هم توصیف کنند.»
وی اشاره کرد که نسخه خاصی از اسپینورها توسعهیافته توسط راجر پنروز (برنده نوبل) و ولفگانگ ریدلر، نقش کلیدی در کشف این معادله داشته است.
این دستاورد نهتنها گامی بلند در پیشبرد مرزهای ریاضیات محض به شمار میرود، بلکه بر توانمندی روبهرشد گروه توپولوژی دانشگاه موناش نیز صحه میگذارد؛ گروهی که هماکنون ۹ دانشجوی دکترا را در خود جای داده است و نیمی از آنها را زنان تشکیل میدهند.
ماتیوز اعلام کرد:
«این کشف نمونهای الهامبخش از آن است که مسائل کلاسیک، حتی پس از گذشت قرنها، میتوانند جرقهای برای تولید دانش نوین باشند. باورکردنی نیست مسئلهای که دکارت در قرن هفدهم مطرح کرده است، هنوز هم پاسخهای تازهای در دل خود داشته باشد.»























