یک شکل هندسی چهاروجهی عجیب و منحصربهفرد که از ترکیب مواد هوافضایی مانند الیاف کربن و کاربید تنگستن ساخته شده، موفق شده است معمایی ۶۰ ساله را در حوزه ریاضیات حل کند.
به گزارش تکناک، این شکل هندسی عجیب را اگر صد بار به صورت تصادفی رها کنید، در ۹۹ بار تنها روی یک طرف مشخص قرار میگیرد. اگر این کشف پیش از این محقق شده بود، چهبسا فرودگر قمری Athena در مأموریت خود به دلیل واژگونی ناکام نمیماند.
جان کانوی و ریچارد گای، دو ریاضیدان برجسته برای نخستین بار در سال ۱۹۶۶، ایدهای با عنوان «چهاروجهی مونوستاتیک یکنواخت» مطرح کردند. آنان در پی ساخت شکلی چهاروجهی از یک ماده یکنواخت با توزیع وزنی برابر بودند، که همواره روی یک وجه مشخص به حالت پایدار بازگردد. با وجود این، پژوهشهای چندساله این دو در نهایت به رد این فرضیه منتهی شد؛ چهاروجهی مونوستاتیک یکنواخت وجود ندارد.
اما کانوی در ادامه حدس زد که اگر توزیع وزن در چهاروجهی نامتقارن باشد، امکان تحقق چنین ساختاری وجود دارد. هرچند او این احتمال را مطرح کرد، اما هرگز اثباتی رسمی برای آن منتشر نساخت.
گرگلی آمبروش، معمار و پژوهشگر مجارستانی دههها بعد موفق شد این مسئله را اثبات کند و مدل فیزیکی این شکل هندسی را نیز طراحی و تولید نماید. او با تکیه بر ایدههای اولیه کانوی و با بهرهگیری از روشهای رایانهای، وجود چهاروجهی مونوستاتیک با وزن نامتقارن را به صورت تجربی و ریاضی تأیید کرد.
جان کانوی که در زمینه هندسه و تعادل چندوجهیها شهرتی جهانی داشت، در پژوهشهای خود به دنبال اثبات تعادل اشکال هندسی با خواص ویژه بود. اما باوجود تلاشهای بسیار، ساخت چهاروجهی با توزیع وزن یکنواخت که همواره روی یک وجه پایدار بایستد، ممکن نشد.

با تغییر فرض اولیه و پذیرش توزیع نامتقارن جرم، مسئله بار دیگر به جریان افتاد. پژوهشهایی مشابه در دهه ۲۰۰۰ با کشف شکل هندسی «gömböc» توسط گابور دوموکوش و همکاران او جان تازهای گرفت. شکل gömböc به عنوان نخستین جسم مادی با ویژگی مونوستاتیک واقعی معرفی شد؛ شکلی با سطح پیوسته که صرفاً در دو نقطه (یکی پایدار و دیگری ناپایدار) تعادل دارد.
با وجود این، gömböc یک شکل نرم و گرد است و یک چندوجهی زاویهدار نیست. همین مسئله توجه دوموکوش را به فرضیه فراموششده کانوی جلب کرد: آیا یک چهاروجهی با زوایای مشخص میتواند رفتار مشابهی نشان دهد؟
یکی از دانشجویان معماری دوموکوش به نام گرگلی آمبروش در سال ۲۰۲۲ در قالب پروژهای درسی، با مسئله تعادل چهاروجهیها آشنا شد. او برخلاف محاسبات دستی زمان کانوی، از الگوریتمی رایانهای بهره گرفت تا میلیونها حالت هندسی ممکن را بررسی کند. الگوریتم طراحیشده توسط او در نهایت مختصات رئوس چهاروجهی را استخراج کرد که با اعمال وزنهای مشخص، ویژگی مونوستاتیک از خود نشان میداد.
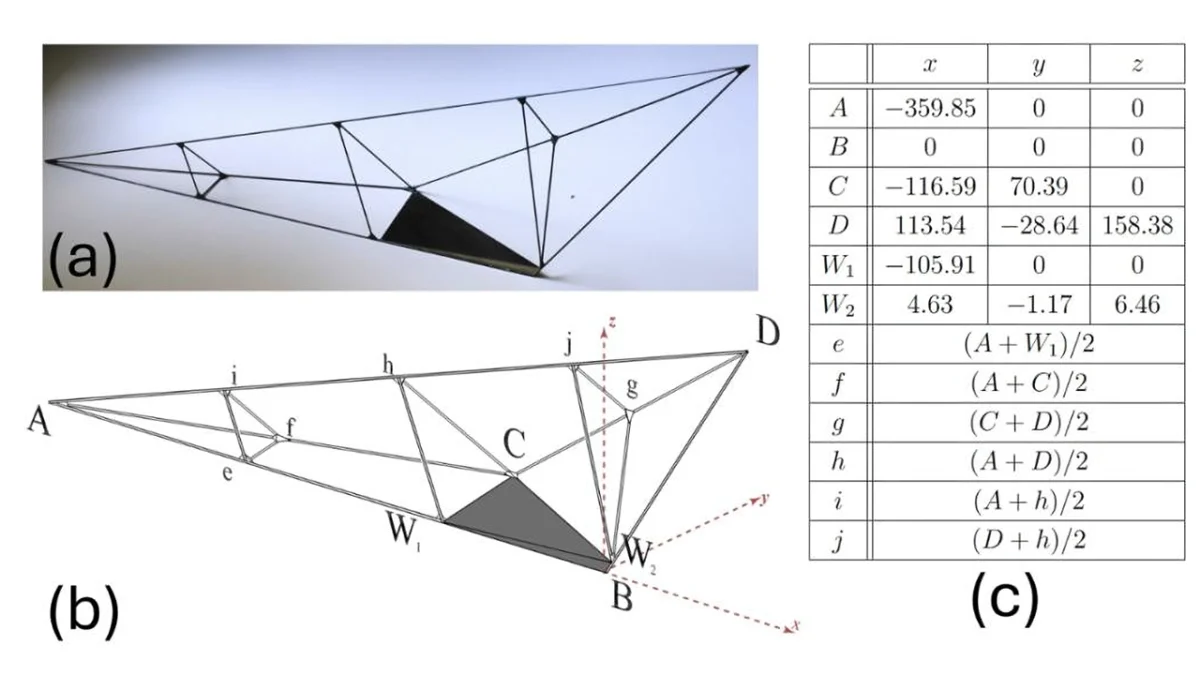
این یافته نهتنها فرضیه کانوی را تأیید کرد، بلکه باعث پرسشهایی جدید شد: آیا تنها یک چهاروجهی با این ویژگی وجود دارد؟ شرایط هندسی موردنیاز برای چنین رفتاری چیست؟
پژوهشهای تکمیلی نشان دادند که برای پایداری مونوستاتیک، سه ضلع متصل باید زاویه باز بسازند و مرکز جرم نیز در یکی از چهار ناحیه موسوم به «منطقه بارگذاری» قرار گیرد. این مناطق، بخشهایی داخلی از چهاروجهی هستند که در صورت قرارگیری مرکز جرم در آنها، جسم همواره روی همان وجه، پایدار خواهد ماند.
با اثبات نظری وجود این ساختار، گام بعدی ساخت مدل فیزیکی آن بود. بر اساس محاسبات، بخشی از این چهاروجهی نیازمند مادهای با چگالی بسیار بالا بود، چنانکه در ابتدا چگالی حدود ۱.۵ برابر هسته خورشید پیشنهاد شد. اما در نهایت راهحل عملیتری بهکار گرفته شد و آن هم استفاده از قاب سبک الیاف کربن و بخش کوچکی از کاربید تنگستن درون ساختاری توخالی بود.
پس از ساخت نمونه، مدل اولیه طبق انتظار عمل نمیکرد، تا اینکه یکی از مهندسان متوجه باقی ماندن تودهای از چسب روی یکی از رئوس شد. پس از پاکسازی آن، مدل بهدرستی کار کرد و چهاروجهی بارها روی وجه پایدار فرود آمد.

کشف این شکل هندس نهتنها گامی بزرگ در اثبات یکی از پیچیدهترین فرضیات هندسی محسوب میشود، بلکه امکان بهرهبرداریهای کاربردی در صنایع مختلف، بهویژه هوافضا را نیز فراهم میسازد. دوموکوش و آمبروش هماکنون مشغول بررسی امکان بهکارگیری این یافته در طراحی فرودگرهای قمری هستند؛ ساختارهایی که در صورت واژگونی، به طور خودکار به حالت ایستاده بازمیگردند.
آمبروش که قرار بود مسیر حرفهای خود را در معماری دنبال کند، با طنز گفت: «من قرار بود معمار شوم… چطور سر از اینجا درآوردم؟» شاید پاسخ این پرسش در یک کلمه خلاصه شود: رایانه.