فهرست مطالب
ریاضیدانان از شاخهای به نام توپولوژی برای مطالعهٔ شکل کیهان و هر آنچه در آن است استفاده میکنند.
به گزارش تکناک، وقتی به محیط اطراف خود نگاه میکنید، ممکن است به نظر برسد که روی یک صفحهٔ مسطح زندگی میکنید. در واقع به همین دلیل است که میتوانید در یک شهر جدید با استفاده از نقشه مسیریابی کنید؛ نقشه یک ورق کاغذ صاف است که همهٔ مکانهای اطراف را نشان میدهد. احتمالاً به همین خاطر برخی از مردم در گذشته تصور میکردند زمین تخت است. اما امروزه بیشتر مردم میدانند که این تصور کاملاً اشتباه است.
شما روی سطح یک کرهٔ غولپیکر زندگی میکنید؛ مانند یک توپ ساحلی به اندازهٔ زمین که اندکی پستی و بلندی دارد. سطح این کره و صفحهٔ تخت هر دو نمونهای از فضاهای ۲بعدی هستند؛ یعنی میتوانید در دو جهت حرکت کنید: شمال-جنوب یا شرق-غرب.
چه فضاهای ممکن دیگری وجود دارند که شما روی آنها زندگی کنید؟ به عبارت دیگر، چه فضاهای دوبعدی دیگری پیرامون شما وجود دارند؟
برای مثال، سطح یک پیراشکی غولپیکر نیز نمونهٔ دیگری از یک فضای ۲بعدی است.
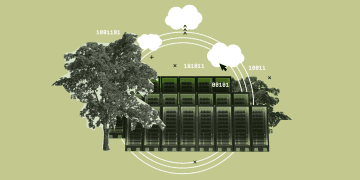
ریاضیدانان از طریق شاخهای به نام توپولوژی هندسی به مطالعهٔ همهٔ فضاهای ممکن در تمام ابعاد میپردازند. توپولوژی همچنین زیربنای مفهومی بسیاری از پروژههای علمی و مهندسی را تشکیل میدهد؛ از جمله:
- طراحی شبکههای حسگر امن،
- دادهکاوی (استخراج اطلاعات از مجموعههای بزرگ داده)،
- استفاده از اُریگامی (هنر کاغذ و تا) برای استقرار ماهوارهها.
01
از 04شکل کیهان
وقتی به اطراف خود نگاه میکنید، فضا را سهبعدی میبینید؛ درست همانطور که سطح زمین یک فضای ۲بعدی به نظر میرسد. اما درست مانند زمین، اگر کل کیهان را بهعنوان یک مجموعه در نظر بگیرید، ممکن است فضای آن بسیار پیچیدهتر باشد؛ برای مثال، شاید کیهان نسخهای سه بعدی و غولپیکر از سطح دوبعدی یک توپ ساحلی باشد یا چیزی حتی عجیبتر از آن.
برای تعیین اینکه شما روی چیزی شبیه یک توپ ساحلی غولپیکر زندگی میکنید نیازی به توپولوژی نیست. با این حال، دانستن تمام فضاهای ۲بعدی ممکن میتواند مفید باشد. بیش از یک قرن پیش، ریاضیدانان همهٔ فضاهای ۲بعدی ممکن و بسیاری از ویژگیهای آنها را شناسایی کردند.

در چند دههٔ گذشته، ریاضیدانان دربارهٔ همهٔ فضاهای ۳بعدی ممکن اطلاعات زیادی بهدست آوردهاند. اگرچه درک ما از فضاهای ۳بعدی به کاملی درک ما از فضاهای ۲بعدی نیست، اما آموختههای فراوانی داریم. فیزیکدانان و ستارهشناسان نیز با تکیه بر این دانش تلاش میکنند مشخص کنند که انسانها واقعاً در کدام فضای ۳بعدی زندگی میکنند.
با اینکه پاسخ این پرسش هنوز بهطور کامل مشخص نیست، گزینههای جذاب و شگفتآور بسیاری وجود دارند. اگر زمان را نیز بهعنوان یک بعد در نظر بگیرید، گزینهها حتی پیچیدهتر میشوند.
برای درک بهتر این موضوع، توجه کنید که برای مشخص کردن مکان یک جرم (مثلاً یک دنبالهدار) در فضا به چهار عدد نیاز دارید: سه عدد برای تعیین موقعیت مکانی آن و یک عدد برای تعیین زمانی که آن جرم در آن موقعیت قرار دارد. این چهار عدد یک فضای چهار بعدی را تشکیل میدهند.
حالا میتوانید فکر کنید که چه فضاهای ۴بعدی ممکن وجود دارند و شما در کدامیک از آنها زندگی میکنید.
02
از 04توپولوژی در ابعاد بالاتر
در این مرحله ممکن است به نظر برسد که نیازی به بررسی فضاهایی با بیش از ۴ بُعد وجود ندارد، زیرا چهار بُعد بیشترین ابعادی است که میتوانیم برای کیهان خود تصور کنیم. اما شاخهای از فیزیک به نام نظریهٔ ریسمان (String Theory) مطرح میکند که کیهان دارای ابعادی به مراتب بیش از چهار است.
علاوه بر این، در نظر گرفتن فضاهایی با ابعاد بالاتر کاربردهای عملی نیز دارد؛ برای مثال، در برنامهریزی حرکت رباتها.
فرض کنید میخواهید حرکت سه ربات را در کف یک کارخانه بررسی کنید:
- کف کارخانه را شبکهبندی کنید و موقعیت هر ربات را با دو مختصهٔ x و y روی این شبکه مشخص کنید.
- از آنجا که هر یک از سه ربات برای تعیین موقعیت به دو مختصه نیاز دارد، در مجموع شش عدد برای توصیف موقعیت همهٔ آنها لازم است.
- میتوانید تمام حالتهای ممکن این سه ربات را بهصورت یک فضای ۶بعدی در نظر بگیرید.
با افزایش تعداد رباتها، بُعد فضای مورد نیاز برای توصیف حرکت آنها نیز افزایش مییابد. همچنین اگر اطلاعات دیگری مانند مکان موانع را هم لحاظ کنید، فضای ممکن حرکت رباتها حتی پیچیدهتر میشود. در نتیجه، برای بررسی چنین مسئلهای باید به مطالعهٔ فضاهای پُربعد بپردازید.
مسائل علمی بیشمار دیگری نیز وجود دارند که در آنها مفهوم فضاهای پُربعد مطرح است؛ از مدلسازی حرکت سیارهها و فضاپیماها گرفته تا درک «شکل» مجموعهدادههای عظیم.
03
از 04گرههای ریاضیاتی
یکی دیگر از مسائلی که توپولوژیستها مطالعه میکنند این است که چگونه یک فضا درون فضای دیگر قرار میگیرد.
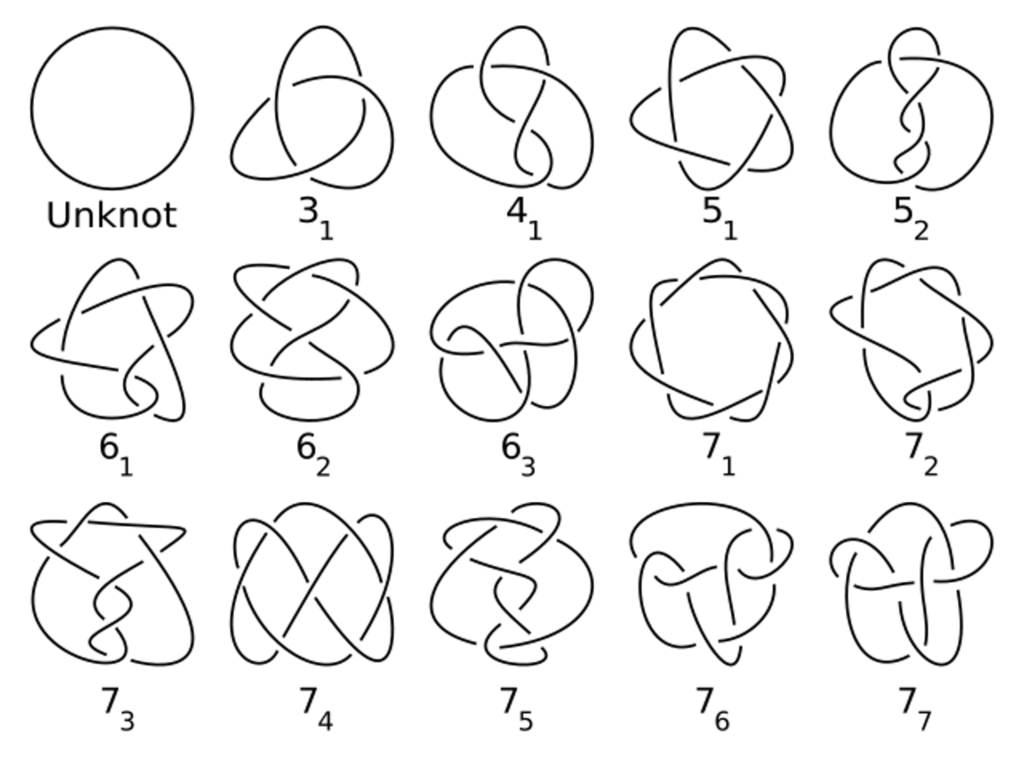
برای مثال، اگر یک حلقهٔ طناب گرهخورده در دست داشته باشید، در واقع یک فضای ۱بعدی (حلقهٔ طناب) درون یک فضای ۳بعدی (اتاق شما) دارید. به چنین حلقههایی «گره ریاضیاتی» گفته میشود.
مطالعهٔ گرهها در ابتدا از علم فیزیک آغاز شد، اما اکنون به یکی از حوزههای اصلی توپولوژی تبدیل شده است. گرهها نقشی اساسی در نحوهٔ درک فضاهای ۳بعدی و ۴بعدی توسط دانشمندان ایفا میکنند و ساختاری جذاب و ظریف دارند که پژوهشگران همچنان در تلاش برای درک کامل آن هستند.
علاوه بر این، گرهها کاربردهای فراوانی دارند؛ از نظریهٔ ریسمان در فیزیک گرفته تا نوترکیبی DNA در زیستشناسی و پدیدهٔ دستسانی در شیمی.
04
از 04شما بر روی چه شکلی زندگی میکنید؟
توپولوژی هندسی شاخهای زیبا و پیچیده است و همچنان پرسشهای هیجانانگیز بیشماری دربارهٔ فضاها بدون پاسخ باقی ماندهاند. برای مثال:
- حدس پوانکارهٔ هموار ۴بعدی این پرسش را مطرح میکند که «سادهترین» فضای بستهٔ ۴بعدی چیست.
- حدس «ورقه-نوار» (slice-ribbon) میکوشد دریابد که چگونه گرهها در فضای سه بعدی با سطوح در فضای چها بعدی ارتباط پیدا میکنند.
توپولوژی در حال حاضر در علوم و مهندسی کاربرد دارد. گشودن رازهای بیشترِ فضاها در همهٔ ابعاد برای درک کیهانی که در آن زندگی میکنیم و حل مشکلات دنیای واقعی بینهایت ارزشمند خواهد بود.